Arranging objects in 2D and 3D

No matter how many (thousand) times you wrote a particular piece of code, you always have to it look up. I’ve been there so many times.

My brain forgets most snippets that involve lots of Math.sin and others. Anything like ((2 * i) / numItems) * PI. Unfortunately, that’s what a lot of “creative coding” is about. Fortunately, my brain can do association, like “I know I wrote this code in that project.”

I now have too many creative code algorithms across too many projects. So I’ve collected them in this article.

All snippets are language-agnostic, framework-agnostic and valid JavaScript.

2D

Arrange in a 2D grid

// arrange items in a horizontal grid from left to right
let gridSize = 5;
let itemSize = 60;
let numItems = 17;

for (let i = 0; i < numItems; i++) {
  // from left to right
  let gx = i % gridSize;
  let gy = Math.floor(i / gridSize);
  // swap gx and gy to arrange in a vertical grid from top to bottom
  // gx = Math.floor(i / gridSize);
  // gy = i % gridSize
  let x = gx * itemSize;
  let y = gy * itemSize;
  // 4px spacing
  rect(x, y, itemSize - 4, itemSize - 4);
}

Arrange in a circle

let numItems = 8;
let radius = 100;
for (let i = 0; i <= numItems; i++) {
  // I love this line
  let angle = ((2 * i) / numItems) * Math.PI;
  let x = Math.cos(angle) * radius;
  let y = Math.sin(angle) * radius;
  ellipse(x, y, 20, 20);
}

Arrange on a half circle

let numItems = 7;
let radius = 100;
// use this value to offset the angle and rotate your semicircle
let angleOffset = 0;
for (let i = 0; i < numItems; i++) {
  let t = i / Math.max(1, numItems - 1);
  let angle = Math.PI * t + angleOffset;
  let x = Math.cos(angle) * radius;
  let y = Math.sin(angle) * radius;
  ellipse(x, y, 20, 20);
}

Make a spiral

let turns = 3; // How many revolutions
let radius = 100;
// How close we want the points to be, as an angle in radians, smaller is closer
let tightness = 0.2;
let full = Math.PI * 2 * turns;

for (let angle = 0; angle < full; angle += tightness) {
  let r = radius * (angle / full);
  let x = Math.cos(angle) * r;
  let y = Math.sin(angle) * r;
  ellipse(x, y, 4, 4);
}

3D

Random points on the surface of a sphere

let radius = 100;

for (let i = 0; i < 1000; i++) {
  // random θ and φ — spherical coordinate stuff 🤷‍♂️
  let theta = random(0, Math.PI * 2);
  let phi = random(-Math.PI / 2, Math.PI / 2);

  let x = radius * Math.sin(theta) * Math.cos(phi);
  let y = radius * Math.sin(theta) * Math.sin(phi);
  let z = radius * Math.cos(theta);
  point(x, y, z);
}

Random points in a sphere

for (let i = 0; i < 1000; i++) {
  let phi = Math.random() * (2 * Math.PI);
  let costheta = Math.random() * 2 - 1;
  let u = Math.random();

  let theta = Math.acos(costheta);
  // Math.cbrt is part of ES2015
  let r = radius * Math.cbrt(u);

  let x = r * Math.sin(theta) * Math.cos(phi);
  let y = r * Math.sin(theta) * Math.sin(phi);
  let z = r * Math.cos(theta);
  point(x, y, z);
}

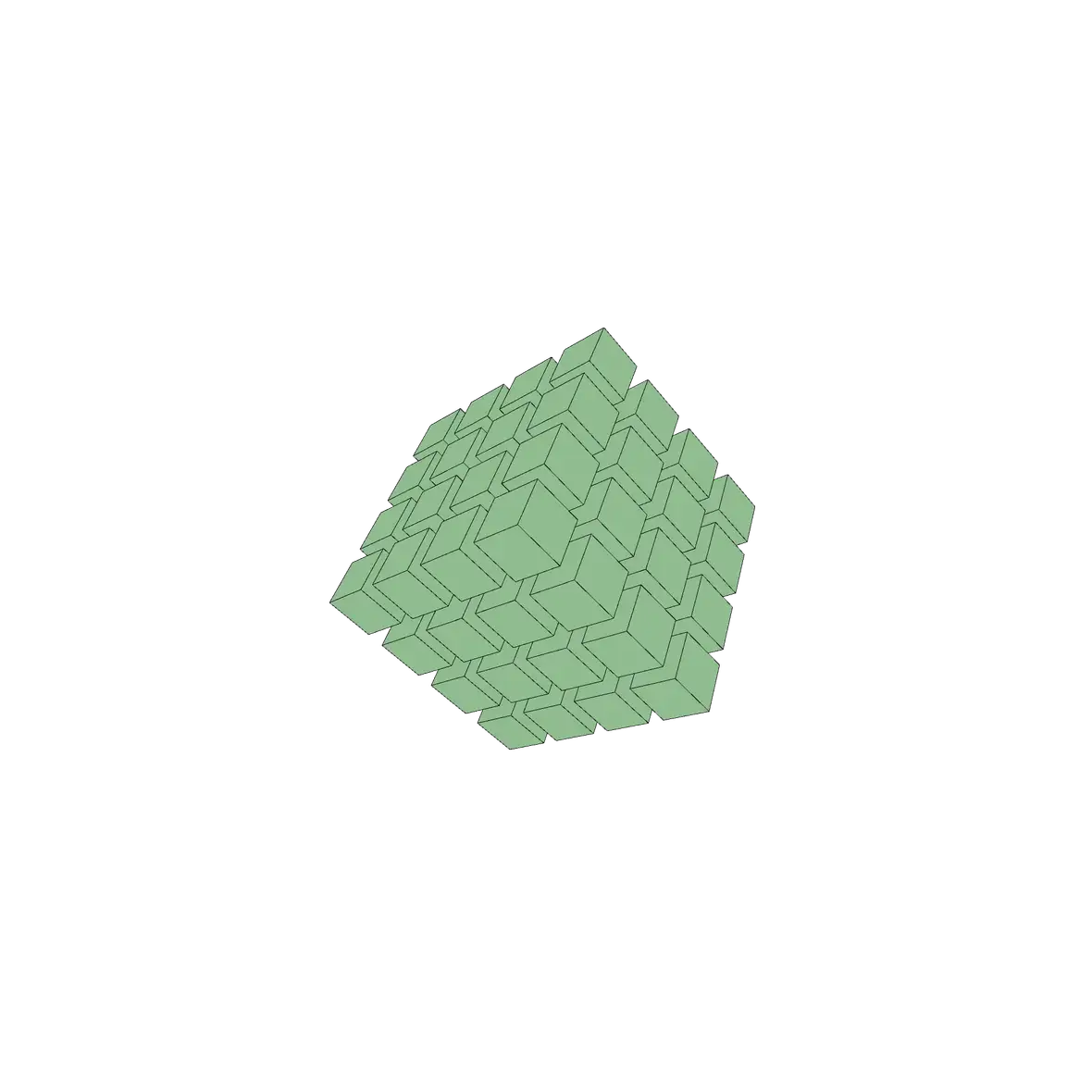
Create a cube of cubes!

let xCount = 4;
let yCount = 4;
let zCount = 4;
let boxSize = 20;

for (let k = 0; k < zCount; k++) {
  for (let j = 0; j < yCount; j++) {
    for (let i = 0; i < xCount; i++) {
      let size = boxSize + 7; // add a bit of spacing around each cube
      let halfWayX = (size * xCount) / 2;
      let halfWayY = (size * yCount) / 2;
      let halfWayZ = (size * zCount) / 2;

      if (xCount % 2 != 0) halfWayX -= size / 2;
      if (yCount % 2 != 0) halfWayY -= size / 2;
      if (zCount % 2 != 0) halfWayZ -= size / 2;

      let x = size * i - halfWayX;
      let y = size * j - halfWayY;
      let z = size * k - halfWayZ;
      box(x, y, z, boxSize, boxSize, boxSize);
    }
  }
}

If you’re curious how these images were generated, the code is available in this repository.

Suggestions welcome! I want to keep updating this post with cool visuals, and I would love your help. Please keep suggestions to spatial stuff though. We collectively wrote enough bubble sorts.